• Point on the side of the plane
• Fast ray-aabb intersection test
• Ray-triangle intersection - Möller–Trumbore
• Ray-triangle intersection - Watertight Ray/Triangle Intersection
• Distance to line (line-line/ray-ray intersection)
• Check if normals “look at” each other
• Ray-plane\line-plane intersection

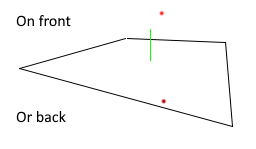
bool Plane::pointOnFront(const Vector4& v)
{
	if( faceNormal.dot(faceCenter - v) < 0.f ) return true;
	return false;
}
					

bool Aabb::rayTest( const Ray& r )
{
	float t1 = (m_min.x - r.m_origin.x)*r.m_invDir.x;
	float t2 = (m_max.x - r.m_origin.x)*r.m_invDir.x;
	float t3 = (m_min.y - r.m_origin.y)*r.m_invDir.y;
	float t4 = (m_max.y - r.m_origin.y)*r.m_invDir.y;
	float t5 = (m_min.z - r.m_origin.z)*r.m_invDir.z;
	float t6 = (m_max.z - r.m_origin.z)*r.m_invDir.z;

	float tmin = std::max(std::max(std::min(t1, t2), std::min(t3, t4)), std::min(t5, t6));
	float tmax = std::min(std::min(std::max(t1, t2), std::max(t3, t4)), std::max(t5, t6));
	
	if (tmax < 0 || tmin > tmax) return false;

	return true;
}
					

bool Triangle::rayTest_MT( const Ray& ray, bool withBackFace, f32& T, f32& U, f32& V, f32& W )
{
	Vector4  pvec = ray.m_direction.cross(e2);
	f32 det  = e1.dot(pvec);
	
	if( withBackFace )
	{
		if( std::fabs(det) < Epsilon )
			return false;
	}
	else
	{
		if( det < Epsilon && det > -Epsilon )
			return false;
	}

	Vector4 tvec(
		ray.m_origin.x - v1.x,
		ray.m_origin.y - v1.y,
		ray.m_origin.z - v1.z,
		0.f);

	f32 inv_det = 1.f / det;
	U = tvec.dot(pvec) * inv_det;

	if( U < 0.f || U > 1.f )
		return false;

	Vector4  qvec = tvec.cross(e1);
	V    = ray.m_direction.dot(qvec) * inv_det;

	if( V < 0.f || U + V > 1.f )
		return false;

	// T is length from origin to intersection point
	T = e2.dot(qvec) * inv_det;
	
	if( T < Epsilon ) return false;
	
	W = 1.f - U - V;
	return true;
}
					

First! Precompute some useful information when you create your ray

inline int max_dim(const Vector4& v)
{
    return (v.x > v.y) ? ((v.x > v.z) 
		? 0 : 2) : ((v.y > v.z) ? 1 : 2);
}
void Ray::update()
{
	// common useful information
	m_direction.x = m_end.x - m_origin.x;
	m_direction.y = m_end.y - m_origin.y;
	m_direction.z = m_end.z - m_origin.z;
	m_direction.normalize();

	m_invDir.x = 1.f / m_direction.x;
	m_invDir.y = 1.f / m_direction.y;
	m_invDir.z = 1.f / m_direction.z;
	m_invDir.w = 1.f / m_direction.w;

	// for watertight
	/*
	//s32 = int
	//f32 = float
	s32 m_kz = 0;
	s32 m_kx = 0;
	s32 m_ky = 0;

	f32 m_Sx = 0.f;
	f32 m_Sy = 0.f;
	f32 m_Sz = 0.f;
	*/
	m_kz = max_dim
	(
		Vector4
		(
			std::abs(m_direction.x),
			std::abs(m_direction.y),
			std::abs(m_direction.z),
			1.f
		)
	);
	
	m_kx = m_kz + 1;
	if( m_kx == 3 )
		m_kx = 0;
	
	m_ky = m_kx + 1;
	if( m_ky == 3 )
		m_ky = 0;

	if( m_direction[m_kz] )
		std::swap(m_kx, m_ky);

	m_Sx = m_direction[m_kx] / m_direction[m_kz];
	m_Sy = m_direction[m_ky] / m_direction[m_kz];
	m_Sz = 1.f / m_direction[m_kz];
}
					

And the algorithm

bool Triangle::rayTest_Watertight( const Ray& ray, bool withBackFace, f32& T, f32& U, f32& V, f32& W )
	{
		const auto A = v2 - ray.m_origin;
		const auto B = v3 - ray.m_origin;
		const auto C = v1 - ray.m_origin;

		const f32 Ax = A[ray.m_kx] - (ray.m_Sx * A[ray.m_kz]);
		const f32 Ay = A[ray.m_ky] - (ray.m_Sy * A[ray.m_kz]);
		const f32 Bx = B[ray.m_kx] - (ray.m_Sx * B[ray.m_kz]);
		const f32 By = B[ray.m_ky] - (ray.m_Sy * B[ray.m_kz]);
		const f32 Cx = C[ray.m_kx] - (ray.m_Sx * C[ray.m_kz]);
		const f32 Cy = C[ray.m_ky] - (ray.m_Sy * C[ray.m_kz]);

		U = (Cx * By) - (Cy * Bx);
		V = (Ax * Cy) - (Ay * Cx);
		W = (Bx * Ay) - (By * Ax);

		if( U == 0.f || V == 0.f || W == 0.f )
		{
			f64 CxBy = (f64)Cx * (f64)By;
			f64 CyBx = (f64)Cy * (f64)Bx;
			U = (f32)(CxBy - CyBx);

			f64 AxCy = (f64)Ax * (f64)Cy;
			f64 AyCx = (f64)Ay * (f64)Cx;
			V = (f32)(AxCy - AyCx);

			f64 BxAy = (f64)Bx * (f64)Ay;
			f64 ByAx = (f64)By * (f64)Ax;
			W = (f32)(BxAy - ByAx);
		}

		if( withBackFace )
		{
			if( (U<0.f || V<0.f || W < 0.f) &&
				(U>0.f || V>0.f || W > 0.f) )
				return false;
		}
		else
		{
			if(U<0.f || V<0.f || W<0.f)
				return false;
		}

		f32 det = U+V+W;

		if(det == 0.f)
			return false;

		const f32 Az = ray.m_Sz * A[ray.m_kz];
		const f32 Bz = ray.m_Sz * B[ray.m_kz];
		const f32 Cz = ray.m_Sz * C[ray.m_kz];
		const f32 Ts = (U*Az) + (V*Bz) + (W*Cz);
		
		if( !withBackFace ) // CULL
		{
			if( Ts < 0.f || Ts > ray.m_tMax*det )
				return false;
		}
		else
		{
			if( det < 0.f && (Ts >= 0.f || Ts<ray.m_tMax*det))
				return false;
			else if(det > 0.f && (Ts<=0.f || Ts >ray.m_tMax*det))
				return false;
		}

		const f32 invDet = 1.f / det;
		U = U*invDet;
		V = V*invDet;
		W = W*invDet;
		T = Ts*invDet;
		if( T < Epsilon)
			return false;
		return true;
	}
};
					

f32 Ray::distanceToLine(const Vector4& lineP0, const Vector4& lineP1)
	{
		Vector4 u = m_end - m_origin;
		Vector4 v = lineP1 - lineP0;
		Vector4 w = m_origin - lineP0;
		u.W = 0.f;
		v.W = 0.f;
		w.W = 0.f;
		f32 a = u.dot();
		f32 b = u.dot(v);
		f32 c = v.dot();
		f32 d = u.dot(w);
		f32 e = v.dot(w);
		f32 D = a*c - b*b;
		f32 sc, tc;

		if( D < Epsilon )
		{
			sc = 0.f;
			tc = (b>c ? d/b : e/c);
		}
		else
		{
			sc = (b*e - c*d) / D;
			tc = (a*e - b*d) / D;
		}

		Vector4 dP = w + (sc*u) - (tc*v);
		dP.W = 0.f;
		return std::sqrt(dP.dot());
	}
					

/*
P0 - point 1
P1 - point 2
N0 - normal 1
N1 - normal 2
*/
kkVector4 P0 = ...; 
kkVector4 P1 = ...;
kkVector4 N0 = ... + P0;
kkVector4 N1 = ... + P1;
kkVector4 delta = P1 - P0;
f32 dp0 = delta.dot(N0);
f32 dp1 = delta.dot(N1);

//printf("%f %f\n", dp0, dp1);
if( dp0 < 0.f && dp1 > 0.f )
{
	new_polygon->Flip();
	new_polygon->CalculateNormals();
}
					

bool Ray::planeIntersection(const miVec4& planePoint, const miVec4& planeNormal, miVec4& ip) {
		float det = (planeNormal.x*m_dir.x) + (planeNormal.y*m_dir.y) + (planeNormal.z*m_dir.z);
		
		if (std::fabs(det) < miEpsilon) return false;

		miVec4 v;
		v.x = planePoint.x - m_origin.x;
		v.y = planePoint.y - m_origin.y;
		v.z = planePoint.z - m_origin.z;

		float t = (planeNormal.x*v.x) + (planeNormal.y*v.y) + (planeNormal.z*v.z);

		t /= det;

		ip = m_origin + t * m_dir;

		return true;
}